文章作者:Tyan
博客:noahsnail.com | CSDN | 简书
0. 测试环境
Python 3.6.9, PyTorch 1.5.0, Numpy 1.16.6
1. Softmax函数
1.1 数学中的Softmax函数
在数学上,尤其是在概率论和相关领域中,Softmax函数,也被称作归一化指数函数,是逻辑函数(Sigmoid函数)的一种推广。在机器学习和深度学习中,Softmax函数的应用非常广泛,常见于分类问题中。
Softmax函数能将一个含任意实数的$K$维向量$\mathbf {z}$“压缩”到另一个$K$维实向量$\sigma(\mathbf {z})$中,使得向量中每一个元素都在$(0,1)$之间,并且所有元素的和为1。Softmax函数的定义如下:$${\sigma (\mathbf {z})}_{j}={\frac {e^{z_j}} {\sum ^{K}_{k=1} e^{z_k}}} \tag{1}$$其中$j=1, …, K.$。假设$K=3$,向量$\mathbf {z}=[z_1, z_2, z_3]=[1, 2, 3]$,则:
$$\begin{array}{l}\
{\sigma (\mathbf {z})}_{1}={\frac {e^{1}} {e^1 + e^2 + e^3}}=\frac {2.72} {30.19}=0.09 \\
{\sigma (\mathbf {z})}_{2}={\frac {e^{2}} {e^1 + e^2 + e^3}}=\frac {7.39} {30.19}=0.24 \\
{\sigma (\mathbf {z})}_{3}={\frac {e^{3}} {e^1 + e^2 + e^3}}=\frac {20.09} {30.19}=0.67
\end{array}$$
上面的计算过程对应的代码实现如下:
1 | import math |
1.2 神经网络中的Softmax
由于Softmax函数可以将分类输出标准化成各个分类的概率分布,且概率和为1。因此在多分类问题中,通常使用Softmax对神经网络的输出结果进行处理。
在卷积神经网络分类中,最后两层通常是全连接层,因此这里用简单的全连接神经网络来模拟网络的最后两层。如下图:
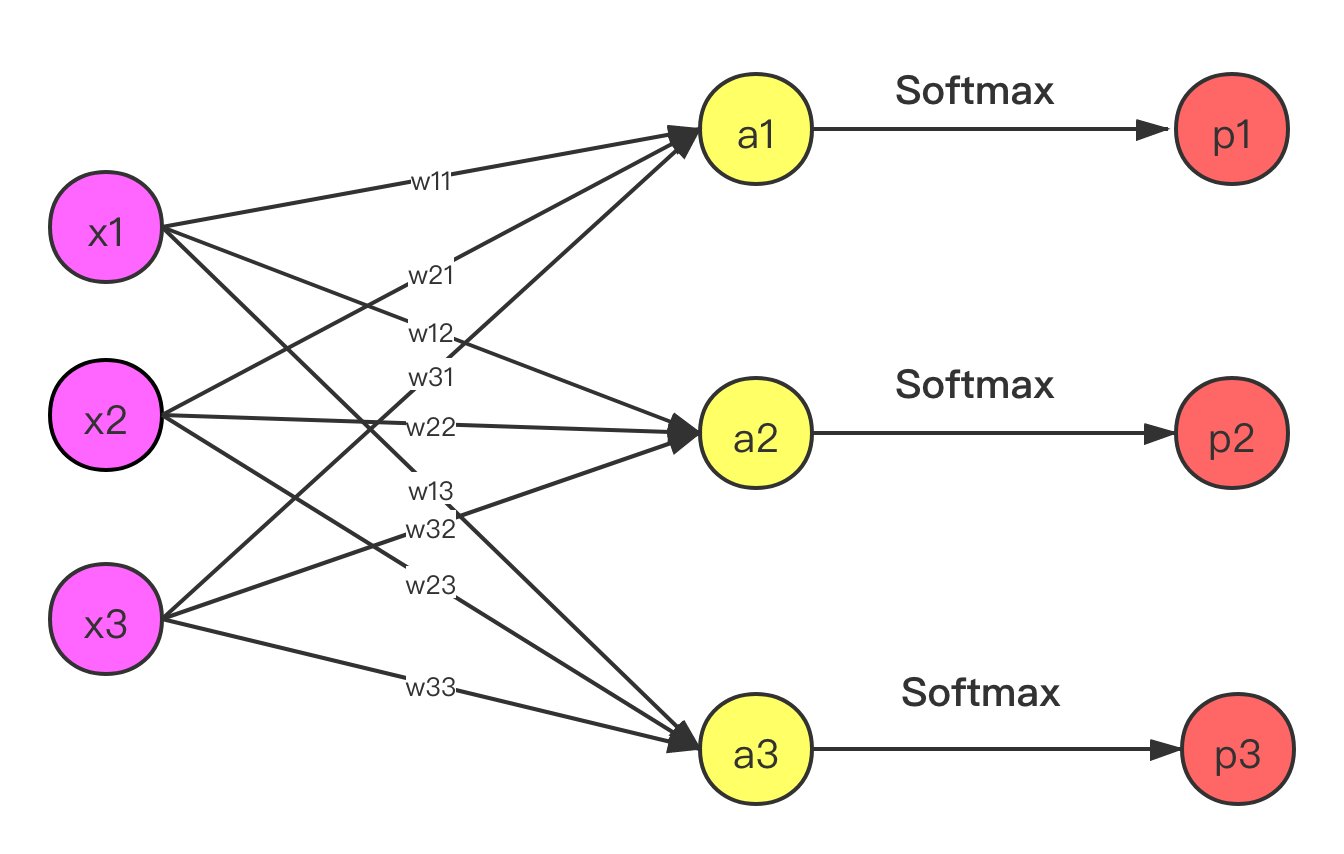
假设问题为一个三分类问题,将图像分为猫、狗、车三类,输入向量$\mathbf{x}=[x_1, x_2, x_3]^T=[1, 2, 3]^T$,$\mathbf{x}$真实标签为车,其标签向量为$\mathbf{y}=[y_1,y_2,y_3]^T=[0, 0, 1]^T$,参数矩阵$$\mathbf{W}=\left [ \begin{array} {l}w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33}\end{array} \right ]=\left [ \begin{array} {l}0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.6 \\ 0.7 & 0.8 & 0.9\end{array} \right ]$$
输出$$\mathbf{a}=\mathbf{Wx}=\left[\begin{array}{l}w_{11}x_1 + w_{12}x_2 + w_{13}x_3 \\ w_{21}x_1 + w_{22}x_2 + w_{23}x_3 \\ w_{31}x_1 + w_{32}x_2 + w_{33}x_3 \end{array}\right]=\left [\begin{array}{l}a_1 \\ a_2 \\ a_3\end{array}\right]=[1.4, 3.2, 5.0]^T$$
对$\mathbf{a}$进行Softmax函数处理后,可得$\mathbf{x}$分类之后的概率输出$$\mathbf{p}=\left [\begin{array}{l} \frac {e^{a_{1}}} {e^{a_{1}} + e^{a_{2}} + e^{a_{3}}} \\ \frac {e^{a_{2}}} {e^{a_{1}} + e^{a_{2}} + e^{a_{3}}} \\ \frac {e^{a_{3}}} {e^{a_{1}} + e^{a_{2}} + e^{a_{3}}} \end{array}\right]=\left [\begin{array}{l}p_1 \\ p_2 \\ p_3\end{array}\right]=[0.02, 0.14, 0.84]^T$$
最终结果如下表所示:
| * | 猫 | 狗 | 车 |
|---|---|---|---|
| y(ground truth) | 0 | 0 | 1 |
| p(prediction) | 0.02 | 0.14 | 0.84 |
这里的Softmax公式为:
2. 交叉熵损失
2.1 交叉熵(cross-entropy)
对于离散分布$p,q$,其交叉熵的定义如下:$$H(p,q)=-\sum ^n_{i=1} p(x_i)\,\log q(x_i) \tag{2}$$
交叉熵来自于信息论中的相对熵(relative entropy),相对熵在概率学和统计学上称为KL散度(Kullback-Leibler divergence),用来度量两个概率分布$p$和$q$的差别。公式如下:$$\begin {array} {l} D_{KL}(p||q)&=\sum ^n_{i=1} p(x_i)log\left(\frac {p(x_i)} {q(x_i)}\right)\\&= \sum ^n_{i=1} p(x_i)log(p(x_i)) - \sum ^n_{i=1} p(x_i)log(q(x_i))\\&=-H(p)+ H(p, q)\end{array}$$
$H(p)$为分布$p$的信息熵,其定义为:$$H(p) = -\sum ^n_{i=1} p(x_i)log(p(x_i))$$
从相对熵的公式上可以看出,其由两部分组成,前一部分为离散分布$p$的信息熵,后一部分为离散分布$p,q$的交叉熵。在图像分类问题中,$p$对应图像的实际分类,其熵是固定的,即KL散度中的$H(p)$不变,因此只需要关注交叉熵即可。
2.2 交叉熵损失函数
由于交叉熵可以度量预测分类和真实分类之间的相似度,因此深度学习中的图像分类经常会用到交叉熵损失函数,其来自交叉熵公式,损失$\mathbf{L}$对应$H(p,q)$,交叉熵的$p(x)$是真实图片类别的概率分布$\mathbf{y}$,即标签向量。$q(x)$是预测图片类别的概率分布,即softmax函数输出的类别概率$\mathbf{p}$。因此单张图片交叉熵损失函数为:$$L=-\sum ^K_{i=1}y_ilog(p_i)\tag{3}$$
$K$是类别数量。$n$张图片的交叉熵损失和为:$$L_{total}=\sum ^{n}_{i=1}L_i \tag{4}$$
在多类别分类问题中(不同于多标签分类),由于图像的实际类别只有一个,因此标签向量为one-hot向量,因此单张图像的交叉熵损失函数会变为:$$L=-y_jlog(p_j)\tag{5}$$
这里的$j$是图像的实际类别,其对应的one-hot向量的第$j$个元素为1,其它为0。代入1.2中的数据到公式3中,由于$y=[0, 0, 1]^T$,因此$\mathbf{x}$交叉熵损失变为:$$\begin {array} {l} L&=-\sum ^K_{i=1}y_ilog(p_i)\\&=-y_1log(p_1)-y_2log(p_2)-y_3log(p_3)\\&=-0*log(0.02) - 0*log(0.14) - 1*log(0.84)\\&=-log(0.84)\\&=0.17 \end {array}$$
这里以$e$为底。
2.3 反向传播
对公式3求偏导:$$\frac {\partial L} {\partial p_{i}} = - \frac {y_i} {p_i}$$
$$\frac {\partial L} {\partial w_{11}} = \frac {\partial L} {\partial p_{1}} \cdot \frac {\partial p_{1}} {\partial a_{1}} \cdot \frac {\partial a_{1}} {\partial w_{11}}$$
$$\frac {\partial L} {\partial p_{1}} = -frac{y_1} {p_1}$$

